Maximum a Posteriori (MAP) vs. Full Bayesian example

The link:

https://haitaodu.wordpress.com/2012/10/05/maximum-a-posteriori-map-vs-bayesian/

Here we want to use an example to illustrate the difference between MAP and Bayesian.

Problem

Suppose we have a jar of coins. There a two types of coins in the jar, type A and type B. For type A coin, if we flip it, we have 60% of getting head (H). For type B it is 40%. In addition, we know there are same number of type A coins and B in the jar.

Someone selected one coin, it could be type A or B, and flipped twice, we got the data $Data=\{H,H\}$ . Given data, we try to make predictions on next flip, i.e.,, we want to know for next coin flip, what is the probability of getting head.

Analysis

We can understand this problem as a parameter estimation problem. We have a discrete distribution, 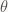$P(H)=\theta$ , $P(T)=1-\theta$ . $\theta$ can only be 0.6 or 0.4, and prior is uniform, which is $P(\theta=0.6)=0.5$ , and $P(\theta=0.4)=0.5$

MAP will select the “right parameter for the distribution” / it is a type A coin or type B coin, and make predictions on it. For example, the calculation gives us $P(\theta=0.6|Data)=0.69$ and $P(\theta=0.4|Data)=0.31$ , we know it is more likely to be a type A coin, we will predict next flip with have 0.6 chance head. And note $P(H)=\arg\max_{\theta}P(\theta|D)=0.6$

Bayesian will NOT be interested in get the “right parameter”. But use the distribution of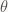 $\theta$ to make the prediction. For example if $P(\theta=0.6|Data)=0.69$ and $P(\theta=0.4|D)=0.31$ , the prediction would be $P(H)=0.69\times0.6+0.31\times0.4=0.538$ , instead of 0.6.

Calculation details

According to Bayes’ Theorem

$\displaystyle P(\theta|Data)= \frac {P(Data|\theta)P(\theta)} {P(Data)}$

Note for given Data, $P(Data)$ is a constant. Therefore we only need to calculate the numerator and normalize it.

$P(Data|\theta=0.6)P(\theta=0.6)=0.6\times0.6\times0.5=0.18$
$P(Data|\theta=0.4)P(\theta=0.4)=0.4\times0.4\times0.5=0.08$

$P(\theta=0.6|Data)=0.18/(0.18+0.08)=0.69$
$P(\theta=0.4|Data)=0.08/(0.18+0.08)=0.31$

Comments

北美加州草坪维护草黄了怎么办

当今中国有句顺口溜，叫做：穷的时候种稻，富的时候种草。我虽然不富，但也种了几年的草。我对种草其实懂得不多，虽自学不辍，但终未成才。不过到底种了几年的草，心得和体会总是有的。现在把我的心得体会写出来，希望对房前屋后有块小草坪的朋友们，不管是穷还是富，都有些帮助。草地上的草，都属于禾本科（Grass Family），与竹子、水稻、小麦、甘蔗和狗尾巴花是同一个科的植物。从个体的数量和分布的范围来讲，禾本科植物应该是植物界最大的科了。草本的禾本科植物通常有两种生长的形态，一种叫蓬草 (bunch grass)，一种叫坪草(sod grass)。用来做草坪的草，当然都是坪草。坪草的物种和品种很多，不同地区不同气候条件种的草不一样，但也有一些共性。一般来说，当地商店里买的草籽（grass seeds）和草皮（ sod），都是比较适合当地的自然条件的。一．维护和保养草坪必做的四件事情 1．割草。定期割草，不仅能使草坪美观，而且也可防止或减缓坪草从营养生长到生殖生长的过渡。营养生长就是长叶子，生殖生长就是开花结籽。很多人都知道，春天的时候有一段时间不割草，草就开花结籽了。大家也见过，边边角角割不到草的地方，那里的草就会开花结籽。 2．浇水。对北美大部分地区来说，春秋天时可视情况少浇水甚至不浇水。草地最需要浇水的时候是夏天，因为夏天最热最干，水分蒸发快。至于浇水要多频繁，那就看你想草地是保绿，还是保命。如果想保绿，那草地每星期得有一英寸的水量。除非有自动浇水系统，浇水是很费时间的，也费钱。我只想我的草地保命，所以我的草地夏天基本不浇水，只在特别容易干死的草地或在特别干旱的年份浇点水。所以到8-9月份的时候，我的草地就黄黄的了，有些难看。不过，一场秋雨来，草地依旧绿。 3．施肥。草地的肥料应以氮素为主，钾素得有一点，但磷的含量可以很低。我用的最多的草坪肥料是30-0- 4。现在有一种运动，推崇不含磷素的草地肥料，因为磷素施用过多，会引起水体（如湖泊，池塘）的富营养化。施肥的话，还是得买个撒肥机（spread er/broadca ster），手持的或手推的型号都行，当地商店都有卖的。没有撒肥机，肥料会撒得很不均匀。 4．杂草...

湾区好吃的中餐馆

一个伪吃货在湾区的checklist 来源：徐聪的日志海鲜： Boiling Crab （San Jose）， Joe's Crab Shack (San Francisco) ， Tomi Sushi & Seafood Buffet（San Jose）， Tatami Sushi & Seafood Buffet（Cupertino）番外：Pier 39 的大螃蟹（San Francisco） Boiling Crab的螃蟹从来都是酒香不怕巷子深，关键在于它家的酱绝对不会让人想起它是一家西餐馆。它家的龙虾也是一绝，当然一旦点了龙虾还打算吃饱的话人均基本在40 刀以上。它家在San Jose有两家分店，如果想避免排长队的话推荐周末中午11点50点以前（12点开门）去101高速边上那家，屡试不爽。 Joe's Crab Shack是一家全美连锁的海鲜餐馆，一锅端 (Steampot) 的吃法很有特色。 Tomi Sushi & Seafood Bufferz中文名叫涛味，排在Tatami之前的原因是它家的口味比较偏中餐，龙虾膏蟹做的不错（不是每天都有）。最近中午去过一次，东西很少，不推荐中午去（虽然价格便宜一些）。 Tatami跟南加著名的Todai都是差不多的日式海鲜自助，生鱼片比较新鲜，不过没有 Todai每小时限量的烤龙虾尾。渔人码头的螃蟹主要的砝码是价格，但跟Boling Crab一比也不见得能便宜多少。有一家摊位上面写着“我们通晓国、粤、英语”，每次都会去。川菜：御食园（San Francisco），金饭碗（Berkeley），红翻天（Foster City），吃香喝辣（Newark），老赵川菜（Mountain View），鹿鸣春（Berkeley），福恩园（ Menlo Park），麻辣诱惑（Fremont），巴山蜀水（Milpitas），福恩园（San Mateo），大四川（Palo Alto），麻辣诱惑（San Jose），山城私房菜（Milpitas ），麻辣帝国（San Mateo）川菜的菜品基本都是那几样，就不单独推荐了。排名第一的Z&Y我觉得就不用...

California life 新手的湾区购房全攻略 (转)

原帖在华人网，感觉写得太全面了，本人非房黑房托，只做技术性讨论，欢迎发表意见第一阶段：全面了解去年12月12号的时候，我正好怀孕37周，冒着风险跨东西海岸大搬家到了Bay。刚下飞机的时候正好下着雨，但是一点也不冷，反而很舒服。来到LG租的apartment，还是吃惊了一小下，因为从Atlanta rent $750 每月 1000sqft的1bed1bath搬到 $1700每月 1000sgft的2bed2bath，这个落差还是比较强烈滴。。。不过呢，既来之则安之，我立马投入了100%的热情开始shopping，布置这个临时的新家来迎接宝宝的出生。要知道在37周之前，我连最基本的crib都没准备，更不用说其他的了。然后就是宝宝出生，出了月子我开始努力换工作，接下来去新公司上班，等到一切稳定下来，大概是4月份的样子，我打算开始做买房的初步了解了。。。首先就是找agent了，一般就是靠熟人推荐。我找的agent优点很明显，经验很丰富，很热情，很耐心，不push，缺点也很明显，就是不太愿承担责任，她会很小心的提供涉及到关键问题的建议，就怕给你产生误导。这样也不是不好，但是对于我们这样没有经验的新手来说，从agent那里拿到的答案总是模棱两可的，我们就很难做出判断。但是 buyer和agent其实就是一个team，买房就是一个teamwork，在这个过程中，通过一次次的沟通，最终我们还是磨合好了。整个过程下来，很难说我们对agent是不是满意，但是只要帮助买到了满意的房子，那就应该是一个好的agent。 4月份和agent初步聊过后，我们当时给出的dream house的条件和大多数刚刚从东部，中西部农村搬来bay的同学基本上是一样的： 1。 SFH，房子要大，1700sqft以上，越新越好，最好2层的。（atlanta 基本配置都是这样的阿。。。） 2。院子小点没关系（在atlanta见过的朋友家的院子都是草坪，就没有精心收拾过的，所以那个时候对后院完全没有概念。。。） 3。学区中等就行，小学800+。（小孩才刚出生，到上学还早呢，如果到时候来不及换房子，那就上私立好了。。。） 4。 commute 30-40分钟都可以。（在atlanta我们还经常开车1个小时去吃饭呢，高速 30分钟也...

Opinion Miner

Search This Blog